Background
Causality is central to many practical data-related questions. Conventional methods for isolating causal relationships rely on experimentation, assume unconfoundedness, or require instrumental variables. However, experimentation is often infeasible, costly, or ethically concerning; good instruments are notoriously difficult to find; and unconfoundedness can be an uncomfortable assumption in many settings.
This article highlights methods for measuring causality beyond these three paradigms. These underappreciated approaches exploit higher moments and heteroscedastic error structures (Lewbel 2012, Rigobon 2003), latent instrumental variables (IVs) (Ebbes et al. 2005), and copulas (Park and Gupta 2012). I will unite them in a common statistical framework and discuss the key assumptions underlying each one.
The focus will be on the ideas, intuition, and practical aspects of these methodologies, rather than technical details. Readers can find more in-depth information in the References section. This article assumes familiarity with econometric endogeneity and the basics of instrumental variables; without this background, some sections may be challenging to follow.
Note: Regression discontinuity (RD) methods are excluded from this discussion, as they fall somewhere between instrument-based and instrument-free econometric methodologies. We know that in fuzzy RDs, the running variable can be viewed as an instrument.
Notation and Setup
Let’s begin by establishing some basic notation. We aim to analyze the impact of a binary, endogenous treatment variable ![]() on an outcome variable
on an outcome variable ![]() , in a setting with exogenous variables
, in a setting with exogenous variables ![]() . We have access to a well-behaved, representative iid sample of size
. We have access to a well-behaved, representative iid sample of size ![]() of
of ![]() , and
, and ![]() . These variables are related as follows:
. These variables are related as follows:
![]()
where ![]() is a mean-zero error term. Our goal is to obtain a consistent estimate of
is a mean-zero error term. Our goal is to obtain a consistent estimate of ![]() . For simplicity, we’re using the same notation for both single- and vector-valued quantities, as
. For simplicity, we’re using the same notation for both single- and vector-valued quantities, as ![]() can be in
can be in ![]() with
with ![]() .
.
The challenge arises because ![]() and
and ![]() are correlated, rendering the standard OLS estimator inconsistent. Even in large samples,
are correlated, rendering the standard OLS estimator inconsistent. Even in large samples, ![]() will be biased, and getting more data would not help. Specifically:
will be biased, and getting more data would not help. Specifically:
![]()
Standard instrument-based methods rely on the existence of an instrumental variable ![]() which, conditional on
which, conditional on ![]() , correlates with
, correlates with ![]() but not with
but not with ![]() . Estimation then proceeds with 2SLS, LIML, or GMM, potentially yielding good estimates of
. Estimation then proceeds with 2SLS, LIML, or GMM, potentially yielding good estimates of ![]() given appropriate assumptions. Common issues with instrumental variables include implausibility of the exclusion restriction, weak correlation with
given appropriate assumptions. Common issues with instrumental variables include implausibility of the exclusion restriction, weak correlation with ![]() , and challenges in interpreting
, and challenges in interpreting ![]() . Formally:
. Formally:
![]()
In this article, we focus on obtaining correct estimates of ![]() in settings where we don’t have access to such an instrumental variable
in settings where we don’t have access to such an instrumental variable ![]() .
.
Diving Deeper
Let’s start with the heteroskedasticity-based approach of Lewbel (2012).
Method 1: Heteroskedasticity & Higher Moments
The main idea here is to construct valid instruments for ![]() by using information contained in the heteroskedasticity of
by using information contained in the heteroskedasticity of ![]() . Intuitively, if
. Intuitively, if ![]() exhibits heteroskedasticity related to
exhibits heteroskedasticity related to ![]() , we can use to create instruments—specifically by interacting
, we can use to create instruments—specifically by interacting ![]() with the residuals of the endogenous regressor’s reduced form equation. So, this is an IV-based method, but the instrument is “internal” to the model and does not rely on any external information.
with the residuals of the endogenous regressor’s reduced form equation. So, this is an IV-based method, but the instrument is “internal” to the model and does not rely on any external information.
The key assumptions are:
- The error term in the structural equation (
 ) is heteroskedastic. This means
) is heteroskedastic. This means 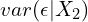 is not constant and depends on
is not constant and depends on 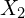 . Moreover, we need
. Moreover, we need 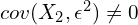 . This is an analogue of the first stage assumption in IV methods.
. This is an analogue of the first stage assumption in IV methods. - The exogenous variable (
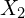 ) are uncorrelated with the product of the endogeneous variable (
) are uncorrelated with the product of the endogeneous variable (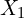 ) and the error term (
) and the error term ( ). That is,
). That is, 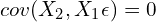 . This is a form of the standard exogeneity assumption in IV estimation.
. This is a form of the standard exogeneity assumption in IV estimation.
The heteroskedasticity-based estimator of Lewbel (2012) proceeds in two steps:
- Regress
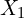 on
on 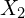 and save the estimated residuals; call them
and save the estimated residuals; call them 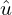 . Construct an instrument for
. Construct an instrument for 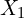 as
as 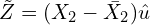 , where
, where 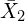 is the mean of
is the mean of 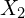 .
. - Use
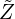 as an instrument in a standard 2SLS estimation:
as an instrument in a standard 2SLS estimation:
![]()
where ![]() is the projection matrix onto the instrument.
is the projection matrix onto the instrument.
This line of thought can also be extended to use higher moments as an alternative or additional way to construct instrumental variables. The original approach uses the variance of the error term, but we can also rely on skewness, kurtosis, etc. The assumptions then must be modified such that these higher moments are correlated with the endogenous variable, etc.
Software Packages: REndo, ivlewbel.
Let’s now move to the second set of methods.
Method 2: Latent IVs
The latent IV approach imposes distributional assumptions on the exogenous part of the endogenous variable and employs likelihood-based methods to estimate ![]() .
.
Let’s simplify the model above, so that we have:
![]()
where ![]() is endogenous. The key idea is to decompose
is endogenous. The key idea is to decompose ![]() into two components:
into two components:
![]()
with ![]() ,
, ![]() , and
, and ![]() . The first condition states that
. The first condition states that ![]() is the exogenous part of
is the exogenous part of ![]() , and the last one gives rise to the endogeneity problem.
, and the last one gives rise to the endogeneity problem.
We then proceed with adding distributional assumptions. Importantly, ![]() must follow some discrete distribution with a finite number of mass points. A common example imposes:
must follow some discrete distribution with a finite number of mass points. A common example imposes:
![]()
and
![]()
These set of assumptions lead to analytical solutions for the conditional and unconditional distributions of ![]() and all parameters of the model are identified. Maximum likelihood estimation can then give us an estimate of
and all parameters of the model are identified. Maximum likelihood estimation can then give us an estimate of ![]() .
.
Software Packages: REndo.
Finally, we turn our attention to the final set of instrument-free methods to solve endogeneity.
Method 3: Copulas
First, a word on copulas. A copula is a multivariate cumulative distribution function (CDF) with uniform marginals on ![]() . An old theorem states that any multivariate CDF can be expressed with uniform marginals and a copula function that represents the relationship between the variables. Specifically, if
. An old theorem states that any multivariate CDF can be expressed with uniform marginals and a copula function that represents the relationship between the variables. Specifically, if ![]() and
and ![]() are two random variables with marginal CDFs
are two random variables with marginal CDFs ![]() and
and ![]() and joint CDF
and joint CDF ![]() , then there exists a copula
, then there exists a copula ![]() such that
such that ![]() .
.
How does this fit into our context and framework? Park and Gupta (2012) introduced two estimation methods for ![]() under the assumption that
under the assumption that ![]() . The key idea is positing a Gaussian copula to link the marginal distributions of
. The key idea is positing a Gaussian copula to link the marginal distributions of ![]() and
and ![]() and obtain their joint distribution. We can then estimate
and obtain their joint distribution. We can then estimate ![]() in one of two ways: either impose distributional assumptions on these marginals and derive and maximize the joint likelihood function of
in one of two ways: either impose distributional assumptions on these marginals and derive and maximize the joint likelihood function of ![]() and
and ![]() , or use a generated regressor approach. We will focus on the latter.
, or use a generated regressor approach. We will focus on the latter.
In the linear model, endogeneity is tackled by creating a novel variable ![]() and adding that as a control (i.e., a generated regressor). Using our simplified model where
and adding that as a control (i.e., a generated regressor). Using our simplified model where ![]() is single-valued and endogenous, we now have:
is single-valued and endogenous, we now have:
![]()
where ![]() is the error term in this augmented model.
is the error term in this augmented model.
We construct ![]() as follows:
as follows:
![]()
Here ![]() is the inverse CDF of the standard normal distribution and
is the inverse CDF of the standard normal distribution and ![]() is the marginal CDF of
is the marginal CDF of ![]() . We can estimate the latter using the empirical CDF by sorting the observations in ascending order and calculating the proportion of rows with smaller values for each observation. As you can guess, this introduces further uncertainty into the model, so the standard errors should be estimated using bootstrap.
. We can estimate the latter using the empirical CDF by sorting the observations in ascending order and calculating the proportion of rows with smaller values for each observation. As you can guess, this introduces further uncertainty into the model, so the standard errors should be estimated using bootstrap.
Software Packages: REndo, copula.
Comparison
Each statistical method has its strengths and limitations. While the methods described here circumvent the traditional unconfoundedness and external instruments-based assumptions, they do not provide a magical panacea to the endogeneity problem. Instead, they rely on their own, different assumptions. These methods are not universally superior, but should be considered when traditional approaches do not fit your context.
The heteroskedasticity-based approach, as the name suggests, requires a considerable degree of heteroskedasticity to perform well. Latent IVs may offer efficiency advantages but come at the cost of imposing distributional assumptions and requiring a group structure of ![]() . The copula-based approach, while simple to implement, also requires strong assumptions about the distributions of
. The copula-based approach, while simple to implement, also requires strong assumptions about the distributions of ![]() and
and ![]() , as well as their relationship.
, as well as their relationship.
That’s it. You are now equipped with a set of new methods designed to identify causal relationships in your data.
Bottom Line
- Conventional methods used to tease causality rely on experiments or ambitious assumptions such as unconfoudedness or the access to valid instrumental variables.
- Researchers have developed methods aimed at measuring causality without relying on these frameworks.
- None of these are a panacea and they rely on their own assumptions that have to be checked on a case-by-case basis.
Where to Learn More
Ebbes, Wedel, and Bockenholt (2009), Park and Gupta (2012), Papies, Ebbes, and Heerde (2017), and Rutz and Watson (2019) provide detailed comparisons of these IV-free methods with alternative methods.
Also, Qian et al. (2024) and Papadopolous (2022) and Baum and Lewbel (2019) have a practical angle that many data scientist will find accessible and attractive.
References
Baum, C. F., & Lewbel, A. (2019). Advice on using heteroskedasticity-based identification. The Stata Journal, 19(4), 757-767.
Ebbes, P. (2004). Latent instrumental variables: a new approach to solve for endogeneity.
Ebbes, P., Wedel, M., & Böckenholt, U. (2009). Frugal IV alternatives to identify the parameter for an endogenous regressor. Journal of Applied Econometrics, 24(3), 446-468.
Ebbes, P., Wedel, M., Böckenholt, U., & Steerneman, T. (2005). Solving and testing for regressor-error (in) dependence when no IVs are available: With new evidence for the effect of education on income. Quantitative Marketing and Economics, 3, 365-392.
Erickson, T., & Whited, T. M. (2002). Two-step GMM estimation of the errors-in-variables model using high-order moments. Econometric Theory, 18(3), 776-799.
Gui, R., Meierer, M., Schilter, P., & Algesheimer, R. (2020). REndo: An R package to address endogeneity without external instrumental variables. Journal of Statistical Software.
Hueter, I. (2016). Latent instrumental variables: a critical review. Institute for New Economic Thinking Working Paper Series, (46).
Lewbel, A. (1997). Constructing instruments for regressions with measurement error when no additional data are available, with an application to patents and R&D. Econometrica, 1201-1213.
Lewbel, A. (2012). Using heteroscedasticity to identify and estimate mismeasured and endogenous regressor models. Journal of business & economic statistics, 30(1), 67-80.
Papadopoulos, A. (2022). Accounting for endogeneity in regression models using Copulas: A step-by-step guide for empirical studies. Journal of Econometric Methods, 11(1), 127-154.
Papies, D., Ebbes, P., & Van Heerde, H. J. (2017). Addressing endogeneity in marketing models. Advanced methods for modeling markets, 581-627.
Park, S., & Gupta, S. (2012). Handling endogenous regressors by joint estimation using copulas. Marketing Science, 31(4), 567-586.
Rigobon, R. (2003). Identification through heteroskedasticity. Review of Economics and Statistics, 85(4), 777-792.
Qian, Y., Koschmann, A., & Xie, H. (2024). A Practical Guide to Endogeneity Correction Using Copulas (No. w32231). National Bureau of Economic Research.
Rigobon, R. (2003). Identification through heteroskedasticity. Review of Economics and Statistics, 85(4), 777-792.
Rutz, O. J., & Watson, G. F. (2019). Endogeneity and marketing strategy research: An overview. Journal of the Academy of Marketing Science, 47, 479-498.
Tran, K. C., & Tsionas, E. G. (2015). Endogeneity in stochastic frontier models: Copula approach without external instruments. Economics Letters, 133, 85-88.
Leave a Reply