Background
Suppose you are working on a project where the relationship between two variables is influenced by an unobserved confounder, and you want to simulate data that reflects this dependency. Standard random number generators often assume independence between variables, making them unsuitable for this task. Instead, you need a method to introduce specific correlations into your data generation process.
A powerful and efficient way to achieve this is through Cholesky decomposition. By decomposing a correlation matrix into its triangular components, you can transform independent random variables into correlated ones. This approach is versatile, efficient, and mathematically grounded, making it ideal for simulating realistic datasets with predefined (linear) relationships.
Diving Deeper
Algorithm
Assume we want to generate a vector ![]() with
with ![]() observations and
observations and ![]() variables with a target correlation matrix
variables with a target correlation matrix ![]() . The algorithm to obtain
. The algorithm to obtain ![]() is as follows:
is as follows:
- Start with Independent Variables: Create a matrix
 of dimensions
of dimensions 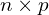 , where each column is independently drawn from
, where each column is independently drawn from 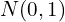 :
: 
- Decompose the Target Matrix: Perform Cholesky decomposition on the target correlation matrix
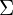 as:
as: ![Rendered by QuickLaTeX.com \[\Sigma = LL^T,\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-952f3dedaa1fa9f4f07b43739a894f75_l3.png)
where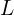 is a lower triangular matrix.
is a lower triangular matrix. - Transform the Independent Variables: Multiply the independent variable matrix
 by
by 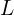 to obtain the correlated variables:
to obtain the correlated variables: ![Rendered by QuickLaTeX.com \[Y = XL.\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-efcce26e82d3dc3c2cd702c53c4e3412_l3.png)
Here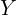 is an
is an 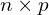 matrix where the columns have the desired correlation structure defined by
matrix where the columns have the desired correlation structure defined by 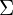 .
.
To ensure that ![]() is a valid correlation matrix, it must be positive-definite. This condition guarantees the success of Cholesky decomposition and the correctness of the resulting correlated variables.
is a valid correlation matrix, it must be positive-definite. This condition guarantees the success of Cholesky decomposition and the correctness of the resulting correlated variables.
Mathematical Explanation
Let’s examine how and why this approach works. We know that ![]() and
and ![]() by definition. We want to show that
by definition. We want to show that ![]() . Here is the simplest way to get there:
. Here is the simplest way to get there:
![]()
There you have it – the algorithm outlined above is mathematically grounded. The covariance matrix of ![]() is indeed equal to
is indeed equal to ![]() . Let’s now look at an example.
. Let’s now look at an example.
An Example
Let’s implement this in R with ![]() and
and ![]() . Our target correlation matrix defines the desired relationships between the variables in
. Our target correlation matrix defines the desired relationships between the variables in ![]() . In our example, we have pairwise correlations equal to 0.8 (b/w
. In our example, we have pairwise correlations equal to 0.8 (b/w ![]() and
and ![]() ), 0.5 (b/w
), 0.5 (b/w ![]() and
and ![]() ), and 0.3 (b/w
), and 0.3 (b/w ![]() and
and ![]() ).
).
rm(list=ls())
set.seed(1988)
# Generate X, independent standard normal variables
n <- 1000
p <- 3
x <- matrix(rnorm(n * p), nrow = n, ncol = p)
# Define Sigma, the target correlation matrix
sigma <- matrix(c(
1.0, 0.8, 0.5,
0.8, 1.0, 0.3,
0.5, 0.3, 1.0
), nrow = p, byrow = TRUE)
# Cholesky decomposition
L <- t(chol(sigma))Using our notation above we have:

The chol function in R decomposes the matrix into a lower triangular matrix. In our example:

Multiplying the independent variables ![]() by the transpose of
by the transpose of ![]() ensures the output
ensures the output ![]() matches the specified correlation structure.
matches the specified correlation structure.
diag <- diag(c(1,1,1))
y <- t(diag %*% L %*% t(x))The cor function checks whether the generated data conforms to the target correlation matrix.
print(round(cor(y), 2))
[,1] [,2] [,3]
[1,] 1.00 0.79 0.51
[2,] 0.79 1.00 0.30
[3,] 0.51 0.30 1.00
print(sigma)
[,1] [,2] [,3]
[1,] 1.0 0.8 0.5
[2,] 0.8 1.0 0.3
[3,] 0.5 0.3 1.0The two matrices match almost exactly. We can also visualize the three variables in a scatterplot matrix. Notice that higher correlation values (e.g., b/w ![]() and
and ![]() correspond to stronger linear associations between.
correspond to stronger linear associations between.
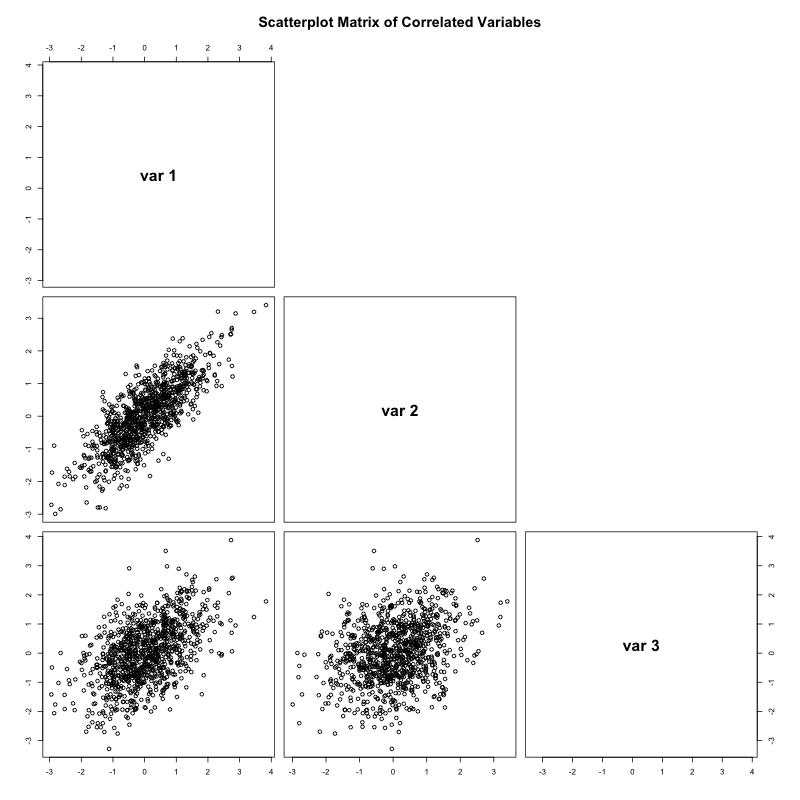
You can find the code in this GitHub repo.
Bottom Line
- A common data practitioner’s need is to generate variables with a predefined correlation structure.
- Cholesky decomposition offers a powerful and efficient way to achieve this.
Leave a Reply