Background
Every dataset inevitably contains missing or incomplete values. Practitioners then face the dilemma of how to address these missing observations. A common approach, though potentially problematic, is to simply ignore them. I am guilty of doing this all too often. While convenient, ignoring missing data can introduce bias into analyses, particularly if the missingness is not entirely random. Moreover, throwing away data usually results in loss of statistical precision. Traditional methods for handling missing data, such as mean or median imputation, usually oversimplify the underlying data-generating process. Regression-based adjustments offer some improvement, but they rely on the linearity assumption.
This article introduces Markov Chain Monte Carlo (MCMC) as a robust and theoretically sound methodology for addressing missing data. Unlike arbitrary imputation methods, MCMC leverages the inherent information within the dataset to generate plausible values for the missing observations. The core principle of MCMC involves treating missing data as random variables and employing the algorithm to sample from their posterior distribution, thereby capturing the uncertainty and built-in structure within the data. The use of MCMC to draw observations repeatedly in the context of missing data is often referred to as Multiple Imputation (MI).
Let’s break this down step by step, explore the underlying intuition, as well as an illustrative example, assuming a basic understanding of probability theory and Bayesian methods.
Notation
To keep things precise, let’s set up some notation. Let ![]() be the complete dataset, which we wish we had. We observe some, but not all observations of
be the complete dataset, which we wish we had. We observe some, but not all observations of ![]() . Let’s split it into observed data
. Let’s split it into observed data ![]() , and missing (or incomplete) data
, and missing (or incomplete) data ![]() , so that
, so that ![]() .
.
Assume a model for the data parameterized by ![]() , that is
, that is ![]() . A simple example would be that a univaraite
. A simple example would be that a univaraite ![]() is Gaussian with some unspecified mean and variance. Our goal is to estimate and fill in
is Gaussian with some unspecified mean and variance. Our goal is to estimate and fill in ![]() by sampling from the posterior distribution
by sampling from the posterior distribution
![]()
The results and intuition hold also conditional on some covariates ![]() , but for simplicity’s sake, I will keep that out of the notation for now.
, but for simplicity’s sake, I will keep that out of the notation for now.
Diving Deeper
Definition
Markov Chain Monte Carlo is a powerful computational technique designed to draw observations from complex probability distributions that are difficult to directly sample from. This might happen because they do not have a nice closed-form analytical expression, or they do, but it’s too messy. Such distributions often arise in Bayesian statistics, where we aim to estimate the posterior distribution of parameters given observed data.
The “magic” of MCMC lies in its iterative nature. It begins with an initial guess for the parameter ![]() . Then, a sophisticated sampling algorithm, such as the Metropolis-Hastings or Gibbs sampler, is employed to generate a sequence of observations. These observations are not independent but are related to each other in a specific way, forming a Markov chain. Crucially, under certain conditions, this Markov chain will eventually converge to the true target distribution.
. Then, a sophisticated sampling algorithm, such as the Metropolis-Hastings or Gibbs sampler, is employed to generate a sequence of observations. These observations are not independent but are related to each other in a specific way, forming a Markov chain. Crucially, under certain conditions, this Markov chain will eventually converge to the true target distribution.
In the context of missing data, MCMC iteratively alternates between the I- and the P-steps. At the ![]() -th iteration with current guess for
-th iteration with current guess for ![]() denoted
denoted ![]() , these steps are:
, these steps are:
- The I-step (imputation): Draw
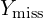 from
from 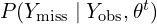 . That is, from its conditional distribution given the observed data and current parameter estimates.
. That is, from its conditional distribution given the observed data and current parameter estimates. - The P-step (posterior): Draw
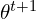 from
from 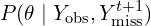 . This is its posterior distribution given the observed data and the newly imputed
. This is its posterior distribution given the observed data and the newly imputed 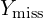 .
.
This back-and-forth dance ensures that the imputed values reflect the uncertainty and structure of the data. And with enough iterations (large ![]() ) the chain will converge to our target,
) the chain will converge to our target, ![]() .
.
Software Packages: mcmc, MCMCPack, mice.
Practical Considerations
Convergence diagnostics are crucial to ensure the MCMC chains have reached a stable equilibrium, as the initial values can significantly influence the results. In simple words, the chain should run long enough so that the posterior distribution does not change significantly after each additional iteration. It is also common to discard (or “burn”) an initial batch of values since they do not come from the final, stable posterior distribution. Additionally, computational costs can be a significant factor, especially for large datasets or complex models but efficient algorithms and parallel processing can help. Lastly, model specification is critical, as the choice of imputation model directly impacts the quality of the imputed values.
An Example
Let’s walk through an example using a simple dataset with missing values. Suppose you have a dataset with two variables, ![]() and
and ![]() , where
, where ![]() , and some values of
, and some values of ![]() are missing. We assume the following relationship:
are missing. We assume the following relationship:
![]()
where ![]() is an error term. We impose priors on
is an error term. We impose priors on ![]() , and
, and ![]() (which collectively comprise
(which collectively comprise ![]() in this exampe).
in this exampe).
We begin with generating some fake data and introduce missingness in ![]() .
.
rm(list=ls())
set.seed(1988)
library(mice)
# generate fake data
n <- 100
c <- 0.2
X <- rnorm(n, mean = 5, sd = 2)
beta0 <- 2
beta1 <- 1.5
epsilon <- rnorm(n, mean = 0, sd = 1)
Y <- beta0 + beta1 * X + epsilon
# introduce missingness in Y
missing_indices <- sample(1:n, size = n * c, replace = FALSE)
Y[missing_indices] <- NA
# combine data into a data frame
data <- data.frame(X = X, Y = Y)
head(data)This is clearly a silly example since ![]() is missing at random, suggesting that missing data does not result in bias. Anyway, for illustration purposes we run the Bayesian Regression algorithm to fill in the missing
is missing at random, suggesting that missing data does not result in bias. Anyway, for illustration purposes we run the Bayesian Regression algorithm to fill in the missing ![]() and proceed with a linear regression of
and proceed with a linear regression of ![]() on
on ![]() .
.
Specifically, the code below uses normal (linear regression) imputation to fill in the missing values. For each missing point the algorithm fits a linear regression model predicting ![]() from
from ![]() using the complete data and then use this model to predict or impute the missing
using the complete data and then use this model to predict or impute the missing ![]() . This process is repeated
. This process is repeated ![]() times (hence the name multiple imputation), creating
times (hence the name multiple imputation), creating ![]() different versions of the dataset with the missing values filled in.
different versions of the dataset with the missing values filled in.
imputed_data <- mice(data,
m = 5,
method = "norm",
seed = 1988)
models <- with(imputed_data, lm(Y ~ X))
summary(pool(models))
term estimate std.error statistic df p.value
1 (Intercept) 1.730583 0.3008046 5.753179 49.51038 5.435802e-07
2 X 1.546689 0.0544164 28.423207 52.02756 2.313802e-33Both coefficients fall in the expected respective regions. You can download the code from this GitHub repo.
Where to Learn More
Following some computational innovations, Bayesian methods have experienced somewhat of a revival in the last 10-15 years. Consequently, there are plenty of high-quality materials online. Takahashi (2017) is an accessible resource on MCMC and Multiple Imputation which I used extensively.
Bottom Line
- Missing data is an ever-present issue in practice.
- Standard approaches to dealing with missing information include ignoring it or imputing it with mean or predicted values.
- MCMC leverages the full joint distribution of the data, making it a robust imputation method.
- By alternating between imputing missing values and updating parameters, MCMC aligns imputations with the observed data’s structure.
References
Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. (1995). Bayesian data analysis. Chapman and Hall/CRC.
Rubin, D B 1987 Multiple Imputation for Nonresponse in Surveys. New York, NY: John Wiley & Sons. DOI: https://doi.org/10.1002/9780470316696
Schafer, J L 1997 Analysis of Incomplete Multivariate Data. Boca Raton, FL: Chapman & Hall/CRC. DOI: https://doi.org/10.1201/9781439821862
Scheuren, F 2005 Multiple imputation: How it began and continues. The American Statistician, 59(4): 315–319.
Takahashi, M. (2017). Statistical inference in missing data by MCMC and non-MCMC multiple imputation algorithms: Assessing the effects of between-imputation iterations. Data Science Journal, 16, 37-37.
Leave a Reply