Stein’s Paradox: A Simple Illustration

Share this article

[This blog post concludes a series of explorations of commonly observed “mysteries” in data science – see also my entries on Lord’s paradox, and Simpson’s paradox.]

Background

In the realm of statistics, few findings are as counterintuitive and fascinating as Stein’s paradox. It defies our common sense about estimation and provides a glimpse into the potential of shrinkage estimators. For aspiring and seasoned data scientists, grasping Stein’s paradox is not merely about memorizing an oddity—it’s about recognizing the delicate balance inherent in statistical decision-making.

In essence, Stein’s paradox asserts that when estimating the means of multiple variables simultaneously, it’s possible to achieve better results compared to relying solely on the sample averages.

Let’s now delve deeper into this statement and unravel the underlying mechanisms.

Diving Deeper

Refresher on Mean Squared Error (MSE)

To understand the paradox, let’s begin by quantify what we mean by “better” estimation. The MSE of an estimator $\hat{\mu}$ is defined as its expected squared error (or loss):

$\text{MSE}(\hat{\mu}) = \mathbb{E}\left[ ( \hat{\mu} - \mu )^2 \right],$

where $\mu = (\mu_1, \mu_2, \dots, \mu_p)$ is the true vector of means. All else equal, the lower MSE the better.

Mathematical Formulation

Stein’s paradox arises in the context of estimating multiple parameters simultaneously. Suppose you’re estimating the mean $\mu_i$ of several independent normal distributions:

$X_i \sim N(\mu_i, \sigma^2), \quad i = 1, \dots, p,$

where $X_i$ are observed values, $\mu_i$ are the unknown means, and $\sigma^2$ is known. We assume non-zero covariance between the variables.

A natural approach is to estimate each $\mu_i$ using its corresponding sample mean $X_i$ , which is the maximum likelihood estimator (MLE). However, in dimensions $p \geq 3$ , this seemingly reasonable approach is dominated by an alternative method.

The surprise? Shrinking the individual estimates toward a common value—such as the overall mean—produces an estimator with uniformly lower expected squared error.

The MSE of the MLE is equal to:

$R(\hat{\mu}_\text{MLE}) = p\sigma^2.$

Now consider the biased(!) James-Stein (JS) estimator:

$\hat{\mu}_\text{JS} = \left( 1 - \frac{(p - 2)\sigma^2}{\lVert X \rVert^2} \right) X,$

where $\lVert X \rVert^2 = \sum_i X_i^2$ is the squared norm of the observed data. The shrinkage factor $1 - \frac{(p - 2)\sigma^2}{|X|^2}$ pulls the estimates toward zero (or any other pre-specified point).

Remarkably, the James-Stein estimator has lower MSE than the MLE for $p \geq 3$ :

$\text{MSE}(\hat{\mu}_{\text{JS}}) < \text{MSE}(\hat{\mu}_{\text{MLE}}).$

This is the mystery at its core.

Why the Paradox?

This result holds because the James-Stein estimator balances variance reduction and bias introduction in a way that minimizes overall MSE. The MLE, in contrast, does not account for the possibility of shared structure among the parameters. The counterintuitive nature of this result stems from the independence of the $X_i$ ‘s. Intuition suggests that pooling information across independent observations should not improve estimation, yet the James-Stein estimator demonstrates otherwise.

An Example

Let’s emulate this paradox in R in a setting with $p=5$ .

rm(list=ls())
set.seed(1988)

p <- 5  # Number of means
n <- 1000  # Number of simulations
sigma <- 1
mu <- rnorm(p, mean = 5, sd = 2)  # True means

# results storage
mse_mle <- numeric(n)  
mse_js <- numeric(n)

We have set the parameters. Next, we create a fake dataset and compute the MSEs of both the MLE and JS estimator. We repeat this 1,000 times and take the average loss for each estimator.

for (sim in 1:n) {
  # Simulate observations
  X <- rnorm(p, mean = mu, sd = sigma)

  # MLE estimator and its MSE
  mle <- X
  mse_mle[sim] <- sum((mle - mu)^2)

  # James-Stein estimator and its MSE
  shrinkage <- max(0, 1 - ((p - 2) * sigma^2) / sum(X^2))
  js <- shrinkage * X
  mse_js[sim] <- sum((js - mu)^2)
}

Finally, we print the results.

cat("Average MSE of MLE:", mean(mse_mle), "\n")
> Average MSE of MLE: 5.125081 
cat("Average MSE of James-Stein:", mean(mse_js), "\n")
> Average MSE of James-Stein: 5.055019

In this example, average MSE of the James-Stein estimator ( $5.06$ ) is consistently lower than that of the MLE ( $5.13$ ), illustrating the paradox in action.

You can download the code from this GitHub repo.

Bottom Line

Stein’s paradox shows that shrinkage estimators can outperform the MLE in dimensions 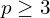$p \geq 3$ , even when the underlying variables are independent.
The James-Stein estimator achieves lower MSE by balancing variance reduction and bias introduction.
Understanding this result highlights the power of shrinkage techniques in high-dimensional statistics.

References

Efron, B., & Hastie, T. (2021). Computer age statistical inference, student edition: algorithms, evidence, and data science (Vol. 6). Cambridge University Press.

2 responses

Lord’s Paradox: A Simple Illustration – yasenov.com

January 10, 2025

[…] of explorations of commonly observed “mysteries” in data science – see also my entries on Stein’s paradox, and Simpson’s […]

Simpson’s Paradox: A Simple Illustration – yasenov.com

January 10, 2025

[…] of explorations of commonly observed “mysteries” in data science – see also my entries on Stein’s paradox, and Lord’s […]