Background
[This article is part of a series of explorations of the limits of statistical models. If the material below is too challenging, I suggest you start here and here.]
The efficiency bound is a cornerstone of the academic literature on semiparametric models, and it’s easy to see why. This bound quantifies the potential loss in efficiency (i.e., increase in variance) that arises when opting for a semiparametric model over a fully parametric one. In doing so, it offers a rigorous benchmark for evaluating the asymptotic variance of any estimator. By providing insights into the trade-offs between model flexibility and statistical precision, the efficiency bound occupies a critical role in understanding the theoretical limits of estimation. Despite its importance, this concept and the broader class of semiparametric models remain underappreciated within much of the data science community.
This article aims to demystify the notion of the semiparametric efficiency bound and its relevance to practical applications. It unpacks the mathematical foundations underlying this concept, shedding light on its relationship with the Cramér-Rao lower bound (CRLB). I will also touch on the bound’s implications for real-world data analysis, where balancing flexibility and efficiency is often a key concern.
Notation
Before diving in, let’s establish the necessary notation to guide our technical discussion. The model governing the data is characterized by parameters ![]() and
and ![]() with likelihood
with likelihood ![]() . Moreover:
. Moreover:
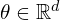 is the parameter of interest, a finite-dimensional vector we want to estimate. Often
is the parameter of interest, a finite-dimensional vector we want to estimate. Often 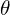 is a scalar. It represents the parametric component of the model.
is a scalar. It represents the parametric component of the model.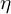 is a nuisance parameter, which is infinite-dimensional (e.g., a nonparametric density or function). It is a nuisance in the sense that it is part of the model, but we are not interested in it for its own sake. It represents the nonparametric component of the model.
is a nuisance parameter, which is infinite-dimensional (e.g., a nonparametric density or function). It is a nuisance in the sense that it is part of the model, but we are not interested in it for its own sake. It represents the nonparametric component of the model.
A leading example is the partially linear model:
![]()
where ![]() is the outcome variable,
is the outcome variable, ![]() represents a vector of covariates,
represents a vector of covariates, ![]() is a function characterized by
is a function characterized by ![]() , while
, while ![]() is an error term. To fit this model in the likelihood notation above, think of
is an error term. To fit this model in the likelihood notation above, think of ![]() as a component of
as a component of ![]() . We assume we have a random i.i.d. sample of all necessary variables.
. We assume we have a random i.i.d. sample of all necessary variables.
Diving Deeper
In semiparametric models, the presence of ![]() complicates the estimation in that it can obscure the relationship between
complicates the estimation in that it can obscure the relationship between ![]() and the observed data. The semiparametric efficiency bound generalizes the CRLB by accounting for the nuisance parameter
and the observed data. The semiparametric efficiency bound generalizes the CRLB by accounting for the nuisance parameter ![]() and isolating the information relevant to
and isolating the information relevant to ![]() .
.
Parametric Submodels
Let’s take a sidestep for a minute. A parametric submodel, say ![]() , that contains
, that contains ![]() alone, represents a subset of distributions that satisfy semiparametric assumptions and contains the true distribution
alone, represents a subset of distributions that satisfy semiparametric assumptions and contains the true distribution ![]() . For any semiparametric estimator that is consistent and asymptotically normal, its asymptotic variance can be compared to the CRLB of the parametric submodel. Since this relationship holds for all possible parametric submodels, the semiparametric estimator’s variance cannot be smaller than any submodel’s bound. In other words, the asymptotic variance of any semiparametric estimator is at least as large as the largest CRLB across all parametric submodels. Informally,
. For any semiparametric estimator that is consistent and asymptotically normal, its asymptotic variance can be compared to the CRLB of the parametric submodel. Since this relationship holds for all possible parametric submodels, the semiparametric estimator’s variance cannot be smaller than any submodel’s bound. In other words, the asymptotic variance of any semiparametric estimator is at least as large as the largest CRLB across all parametric submodels. Informally,
![]()
This is our first insight on the semiparametric efficiency bound, which admittedly is more of theoretical than practical significance.
Efficient Influence Functions
The semiparametric efficiency bound depends on the interplay between ![]() and
and ![]() , captured through the something called the Efficient Influence Function (EIF). Remember that the score function for
, captured through the something called the Efficient Influence Function (EIF). Remember that the score function for ![]() ,
,
![]()
measures the sensitivity of the log-likelihood to changes in ![]() . We can similarly define the score with respect to
. We can similarly define the score with respect to ![]() :
:
![Rendered by QuickLaTeX.com \[S_\eta(X)=\frac{\partial}{\partial \eta} \log f(X; \theta, \eta).\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-a1a4d6038eeaecd8a7d611d5ceba6957_l3.png)
Now enter the EIF ![]() which captures the variation in
which captures the variation in ![]() while adjusting for the nuisance parameter
while adjusting for the nuisance parameter ![]() . It satisfies the orthogonality condition:
. It satisfies the orthogonality condition:
![]()
ensuring that the influence of ![]() is removed from
is removed from ![]() . In other words,
. In other words, ![]() captures only information about
captures only information about ![]() , uncontaminated by nuisance parameters. It is the influence function with the lowest possible variance.
, uncontaminated by nuisance parameters. It is the influence function with the lowest possible variance.
Efficient Score
The next piece of the puzzle is the Efficient Score ![]() , the projection of
, the projection of ![]() onto the space orthogonal to the nuisance tangent space
onto the space orthogonal to the nuisance tangent space ![]() :
:
![]()
where ![]() is the projection operator. Here
is the projection operator. Here ![]() is simply the linear subspace spanned by
is simply the linear subspace spanned by ![]() . The Efficient Score is the part of the score vector that is “free” from the influence of nuisance parameters. It represents the best possible score function for estimating
. The Efficient Score is the part of the score vector that is “free” from the influence of nuisance parameters. It represents the best possible score function for estimating ![]() in the presence of
in the presence of ![]() . (A similar technique underlies the so-called Neyman orthogonality principle in dobule/debiased machine learning.) We can construct the efficient influence function by appropriately scaling the efficient score to get to the optimal EIF.
. (A similar technique underlies the so-called Neyman orthogonality principle in dobule/debiased machine learning.) We can construct the efficient influence function by appropriately scaling the efficient score to get to the optimal EIF.
The Semiparametric Efficiency Bound
We are at last ready to state the main result. The semiparametric efficiency bound is determined by the variance of the Efficient Score:
![Rendered by QuickLaTeX.com \[\text{Var}(\hat{\theta}) \geq \frac{1}{\mathbb{E}[S_\theta^*(X)^2]}.\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-d2704903eea88ccd21047b5e0907aab4_l3.png)
This generalizes the Cramér-Rao lower bound for semiparametric models by incorporating the complexity introduced by the nuisance parameter ![]() . In parametric models, this bound collapses to and is determined by the Fisher Information, while in here, it is governed by the efficient score.
. In parametric models, this bound collapses to and is determined by the Fisher Information, while in here, it is governed by the efficient score.
To achieve the bound in practice, nuisance parameters are often removed through methods like regression residuals, inverse probability weighting, or targeted maximum likelihood estimation (TMLE). These techniques isolate the information about ![]() from
from ![]() , enabling efficient estimation.
, enabling efficient estimation.
Bottom Line
- Semiparametric models blend parametric assumptions (related to a parameter of interest) with nonparametric flexibility (related to nuisance parameters).
- The efficient influence function isolates the information about the parameter of interest, removing the impact of nuisance parameters.
- The semiparametric efficiency bound generalizes CRLB to this class of models. It is determined by the variance of the efficient score vector.
- Practical estimation achieving this bound often involves removing nuisance effects through residualization or other adjustment techniques.
References
Bickel, P. J., Klaassen, C. A., Ritov, Y., & Wellner, J. A. (1993)
Efficient and Adaptive Estimation for Semiparametric Models. Johns Hopkins University Press.
Greene, William H. “Econometric analysis”. New Jersey: Prentice Hall (2000): 201-215.
Hines, O., Dukes, O., Diaz-Ordaz, K., & Vansteelandt, S. (2022). Demystifying statistical learning based on efficient influence functions. The American Statistician, 76(3), 292-304.
Ichimura, H., & Todd, P. (2007) Implementing Nonparametric and Semiparametric Estimators. In Heckman, J. & Leamer, E. (Eds.), Handbook of Econometrics (Vol. 6B).
Newey, W. K. (1990) Semiparametric Efficiency Bounds. Journal of Applied Econometrics, 5(2), 99–135.
Tsiatis, A. (2007). Semiparametric theory and missing data. Springer Science & Business Media
Van der Vaart, A. W. (2000) Asymptotic Statistics. Cambridge University Press.
Leave a Reply