Background
Weights in statistical analyses offer a way to assign varying importance to observations in a dataset. Although powerful, they can be quite confusing due to the various types of weights available. In this article, I will unpack the details behind the most common types of weights used in data science.
Most types of statistical analyses can be performed with weights. These include calculating summary statistics, regression models, bootstrap, etc. Even maximum likelihood estimation is minimally affected. In this article, I will keep it simple and only discuss mean and variance estimation.
The two primary types of weights encountered in practice are sampling weights and frequency weights. I will explore each in turn and conclude with a comparative example.
To begin, let’s imagine a well-behaved random variable ![]() of which we have an iid sample of size
of which we have an iid sample of size ![]() . I will use
. I will use ![]() to denote the relevant weighting variable.
to denote the relevant weighting variable.
Diving Deeper
Mean estimation does not depend on the type of weights. We have:
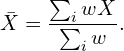
Variance estimation depends on the weight type.
Remember that we estimate the standard error of ![]() as:
as:
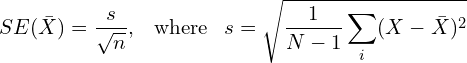
is an estimate of the standard deviation of ![]() . I will explain below how estimation of
. I will explain below how estimation of ![]() differs for sampling and frequency weights. Imporantly,
differs for sampling and frequency weights. Imporantly, ![]() will denote the weighted version of this standard error.
will denote the weighted version of this standard error.
Sampling Weights
Sampling weights measure the inverse probability of an observation entering the sample. They are particularly relevant in surveys when some units in the population are sampled more frequently than others. These weights adjust for sampling discrepancies to ensure that survey estimates are representative of the entire population. Sampling weights are also sometimes called probability weights.
Intuitively, if we want to use the survey to accurately represent the population, we should assign higher importance to observations that are less likely to be sampled and lower importance to those more likely to appear in our data. This is exactly what sampling weights achieve. Sampling weights are, thus, inversely proportional to the probability of selection. Therefore, a smaller weight indicates a higher probability of being sampled, and vice versa.
For example, households in rural areas might be less likely to enter a survey due to the increased resources required to reach remote locations. Conversely, urban households are typically easier to sample and thus more likely to appear in the data.
This weighting approach is also common in causal inference analyses using propensity score methods. Similarly, in machine learning, weighting is often employed to adjust for unbalanced samples in the context of rare events (e.g., fraud detection, cancer diagnosis).
Let’s now get back to the discussion on variance estimation. With sampling weights, we have:
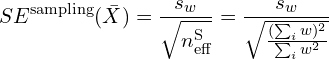
The numerator is the weighted version of the sum of squared deviations from the mean, emphasizing observations with higher weights. The denominator normalizes the standard error based on the total sum of the weights. When the weights differ greatly—high weights make some observations much more influential, increasing uncertainty about the population mean and so the sampling-weighted standard error is often larger.
I will move on to describing frequency weights.
Software Package: survey.
Frequency Weights
Frequency weights measure the number of times an observation should be counted in the analysis. They are most relevant when there are multiple identical observations or when duplicating observations is possible. Naturally, higher weights correspond to observations that appear more frequently. Frequency weights are common in aggregated datasets. For instance, with market- or city-level data, we might want to weight the rows by market size, thus assigning more importance to larger units.
We can gain intuition from a linear algebra perspective. In a regression context, the design matrix ![]() must be of full rank (to ensure invertibility), which implies no two rows can be identical. We thus need to collapse
must be of full rank (to ensure invertibility), which implies no two rows can be identical. We thus need to collapse ![]() to keep only distinct rows and record the number of times each row appears in the original data. This record constitutes the frequency weights.
to keep only distinct rows and record the number of times each row appears in the original data. This record constitutes the frequency weights.
The formula for estimating the standard error of ![]() with frequency weights is:
with frequency weights is:
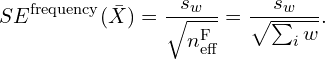
Here ![]() is the effective sample size (i.e., the sum of all weights) and
is the effective sample size (i.e., the sum of all weights) and ![]() is the weighted standard deviation of
is the weighted standard deviation of ![]() .
.
The frequency-weighted standard error is typically the smaller because it increases the effective sample size without introducing variability in the contribution of different observations. In contrast, the sampling-weighted standard error could be larger if some observations are given much higher weights, increasing the variability and lowering the precision.
Software Package: survey
One More Thing
There is actually one more type of weights which are not so commonly used in practice, precision weights. They represent the precision (![]() ) of observations. A weight of 5, for example, reflects 5 times the precision of a weight of 1, originally based on averaging 5 replicate observations. Precision weights often come up in statistical theory in places such as Generalized Least Squares where they promise efficiency gains (i.e., lower variance) relative to traditional Ordinary Least Squares estimation. In practice, precision weights are in fact frequency weights normalized to sum to
) of observations. A weight of 5, for example, reflects 5 times the precision of a weight of 1, originally based on averaging 5 replicate observations. Precision weights often come up in statistical theory in places such as Generalized Least Squares where they promise efficiency gains (i.e., lower variance) relative to traditional Ordinary Least Squares estimation. In practice, precision weights are in fact frequency weights normalized to sum to ![]() . Lastly, Stata’s user guide refers to them as analytic weights.
. Lastly, Stata’s user guide refers to them as analytic weights.
An Example
Let’s see all of this in practice. We begin by creating a fake dataset of a variable ![]() with both sampling and frequency weights. The weights are randomly created and hence have no underlying meaning, so think of this example as a tutorial, without a strong focus on the results.
with both sampling and frequency weights. The weights are randomly created and hence have no underlying meaning, so think of this example as a tutorial, without a strong focus on the results.
library(survey)
rm(list=ls())
set.seed(681)
n <- 100000
data <- data.frame(
x = rnorm(n),
prob_selection = runif(n, .1, .9),
freq_weight = rpois(n, 3)
)
data$samp_weight <- 1 / data$prob_selectionNow let’s calculate the average value of ![]() using both types of weights.
using both types of weights.
design_unweight <- svydesign(ids = ~1, data = data, weights = ~1)
design_samp <- svydesign(ids = ~1, data = data, weights = ~samp_weight)
design_freq <- svydesign(ids = ~1, data = data, weights = ~freq_weight)
mean_unweight <- svymean(~x, design_unweight)
mean_samp <- svymean(~x, design_samp)
mean_freq <- svymean(~x, design_freq)In the code above I assigned the associated weight to a given survey design before computing the means. Now it’s time to see the results.
> print(round(mean_unweight, digits=3))
mean SE
x -0.002 0.0032
> print(round(mean_samp, digits=3))
mean SE
x 0 0.0038
> print(round(mean_freq, digits=3))
mean SE
x -0.002 0.0037The unweighted and frequency-weighted means match exactly, (I am not sure why the sampling-weighted mean is slightly lower.) while the variances are different. The variance with frequency weights is lower than that of sampling weights.
You can find my code in this GitHub repo.
Bottom Line
- Weights are one of the most confusing aspects of working with data.
- Sampling and frequency weights are the most common types of weights found in practice.
- The former measure the inverse probability of being sampled, while the latter represent the number of times an observation enters the sample.
- While weighting usually does not impact point estimates (e.g., regression coefficients, means), incorrect usage of weights can lead to inaccurate confidence intervals and p-values.
- This is relevant only if (i) your dataset contains weights, and (ii) you are interested in population-level statistics.
Where to Learn More
Google is a good starting place. Lumley’s blog post titled Weights in Statistics was incredibly helpful in preparing this article. Stata’s manuals which are publically available contain more detailed information on various types of weighting schemes. See also Solon et al. (2015) for using weights in causal inference.
References
Dupraz, Y. (2013). Using Weights in Stata. Memo, 54(2)
Lumley, T. (2020), Weights in Statistics, Blog Post
Solon, G., Haider, S. J., & Wooldridge, J. M. (2015). What are we weighting for?. Journal of Human resources, 50(2), 301-316.
Stata User’s Guide (2023) https://www.stata.com/manuals/u.pdf
Leave a Reply