Background
[This article is part of a series of explorations of the limits of statistical models. If the material below is too challenging, I suggest you start here.]
Obtaining the lowest possible variance is a primary goal for anyone working with statistical models. Efficiency (or precision), as is the jargon, is a cornerstone of statistics and econometrics, guiding us toward estimators that extract the maximum possible information from the data. It can make or break a data project.
The Cramér-Rao lower bound (CRLB) plays a pivotal role in this context by establishing a theoretical limit on the variance of unbiased estimators. Unbiased estimators are those that yield the true answer (on average), rendering them a highly attractive class of methods. The CRLB highlights the best achievable precision for parameter estimation based on the Fisher information in the data. This article explores the theoretical foundation of the CRLB, its computation, and its implications for practical estimation.
In what follows, I am concerned with unbiased estimators, a common practice that should not be taken for granted. As a counterexample, consider the James-Stein estimator—a biased but attractive technique.
Notation
Before diving in, let’s establish a unified notation to structure the mathematical discussion:
- Let
 denote the observed data, with
denote the observed data, with 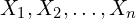 being
being 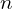 independent and identically distributed (i.i.d.) observations.
independent and identically distributed (i.i.d.) observations. - The model governing the data is characterized by a (finite-dimensional) parameter
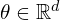 which we aim to estimate.
which we aim to estimate. - The likelihood of the data is
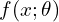 , fully specified by the parameter
, fully specified by the parameter 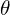 .
.
Diving Deeper
The Cramér-Rao lower bound provides a theoretical benchmark for how precise an unbiased estimator can be. It sets the minimum variance that any unbiased estimator of a parameter ![]() can achieve, given a specific data-generating process.
can achieve, given a specific data-generating process.
The CRLB Formula
For a parameter ![]() in a parametric model with likelihood
in a parametric model with likelihood ![]() , the CRLB is expressed as:
, the CRLB is expressed as:
![]()
where ![]() is the Fisher information (FI), defined as:
is the Fisher information (FI), defined as:
![Rendered by QuickLaTeX.com \[I(\theta) = \mathbb{E}\left[ \left( \frac{\partial}{\partial \theta} \log f(x; \theta) \right)^2 \right].\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-9d8a2a89602348d2628303f18fe1ff98_l3.png)
Intuition
To understand the CRLB, we must delve into the concept of Fisher information named after one of the modern fathers of statistics R.A. Fisher. Intuitively, FI quantifies how much information the observed data carries about the parameter ![]() .
.
Think of the likelihood function ![]() as describing the probability of observing a given dataset
as describing the probability of observing a given dataset ![]() for a particular value of
for a particular value of ![]() . If the likelihood changes sharply with
. If the likelihood changes sharply with ![]() (i.e.,
(i.e., ![]() is large), small changes in
is large), small changes in ![]() lead to noticeable differences in the likelihood. This variability reflects high information: the data can “pinpoint”
lead to noticeable differences in the likelihood. This variability reflects high information: the data can “pinpoint” ![]() with greater precision. Conversely, if the likelihood changes slowly with
with greater precision. Conversely, if the likelihood changes slowly with ![]() , the data offers less information about its true value.
, the data offers less information about its true value.
Mathematically, the Fisher information ![]() is the variance of the the partial derivative
is the variance of the the partial derivative
![]()
which we refer to as the score function. This score measures how sensitive the likelihood function is to changes in ![]() . Higher variance in the score corresponds to more precise information about
. Higher variance in the score corresponds to more precise information about ![]() .
.
Practical Application
The CRLB provides a benchmark for evaluating the performance of estimators. For example, if you propose an unbiased estimator ![]() , you can compare its variance to the CRLB. If
, you can compare its variance to the CRLB. If ![]() , we say the estimator is efficient. However, if the variance is higher, there may be room to improve the estimation method.
, we say the estimator is efficient. However, if the variance is higher, there may be room to improve the estimation method.
Moreover, the CRLB also offers insight into the difficulty of estimating a parameter. If ![]() is “small”, so that the bound on the variance is high, then no unbiased estimator can achieve high precision with the available data. It is possible to develop a biased estimator for
is “small”, so that the bound on the variance is high, then no unbiased estimator can achieve high precision with the available data. It is possible to develop a biased estimator for ![]() with lower variance, but it is not clear why you would do that.
with lower variance, but it is not clear why you would do that.
An Example
Imagine you are estimating the mean ![]() of a normal distribution, where
of a normal distribution, where ![]() , and
, and ![]() is known. The likelihood for a single observation
is known. The likelihood for a single observation ![]() is:
is:
![Rendered by QuickLaTeX.com \[f(x_i;\mu) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x_i-\mu)^2}{2 \sigma^2}}.\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-a170cf35f5959d8afa6c37a567d715ed_l3.png)
Using the Fisher information defintion given above, taking the derivative and simplifying, we find:
![Rendered by QuickLaTeX.com \[I(\mu)= \left( \frac{\partial}{\partial \theta} \log f(x; \theta) \right)^2 = \frac{1}{\sigma^2}.\]](https://yasenov.com/wp-content/ql-cache/quicklatex.com-05acbd2562900f95cee88da3add26dac_l3.png)
For ![]() independent observations, this expression becomes:
independent observations, this expression becomes:
![]()
The CRLB for the variance of any unbiased estimator of ![]() is:
is:
![]()
This result aligns with our intuition: as ![]() increases, the precision of our estimate improves. In other words, more data leads to more informative results.
increases, the precision of our estimate improves. In other words, more data leads to more informative results.
Where to Learn More
Any graduate econometrics textbook will do. Personally, my grad school nightmares were induced by Greene’s textbook (cited below). It can be dry but certainly contains what you need to know.
Bottom Line
- The CRLB establishes a theoretical lower limit on the variance of unbiased estimators, serving as a benchmark for efficiency.
- Fisher information measures the sensitivity of the likelihood to changes in the parameter
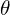 , linking the amount of information in the data to the precision of estimation.
, linking the amount of information in the data to the precision of estimation. - Efficient estimators achieve the CRLB and are optimal under the given model assumptions.
References
Greene, William H. “Econometric analysis”. New Jersey: Prentice Hall (2000): 201-215.
Leave a Reply