Overlapping Confidence Intervals and Statistical (In)Significance

Share this article

Background

This is a mistake I make with data all the time. Even more, I have seen many well-known professors and data masters also fall for it. It goes like this.

I see a graph with two bars depicting two sample means placed right next to each other. The presenter, being a good data scientist, has added error bars representing 95% confidence intervals. The side-to-side placement usually implies that the two quantities are about to be compared. My eyes immediately check whether the two confidence intervals overlap. When they do not, I quickly conclude that the two means are statistically significantly different from each other and, thus, the presenter has uncovered an exciting truth about the world.

This naïve but all too common approach to judging statistical significance is wrong. Here is why.

The Basics of Confidence Intervals

Let’s set up a toy example following Schenker and Gentleman (2001). Imagine we have two quantities – $Y_1$ and $Y_2$ – and we are interested in testing whether they are statistically different from each other. These can stand for US and UK sales or user engagement on Android and iOS devices. For simplicity, we assume all friendly statistical properties (e.g., large and random samples, well-behaved distributions, consistent estimators for all quantities, etc.).

We are interested in whether the population values for $Y_1$ and $Y_2$ are equal. The null hypothesis ( $H_0$ ) states that they indeed are:

(1) $\begin{equation*} $H_0: Y_1 = Y_2$. \end{equation*}$

We will denote our estimates of $Y_1$ and $Y_2$ with $\hat{Y_1}$ and $\hat{Y_2}$ and refer to their estimated standard errors as $\hat{SE}(Y_1)$ and $\hat{SE}(Y_2)$ . The corresponding confidence intervals for $Y$ and $Y_2$ are given by the following:

(2) $\begin{equation*} \hat{Y_1} \pm 1.96 \times \hat{SE}(Y_1) \end{equation*}$

and

(3) $\begin{equation*} \hat{Y_2} \pm 1.96 \times \hat{SE}(Y_2). \end{equation*}$

So far, so good.

Importantly, note that we can also construct a confidence interval for the difference $(Y_1 - Y_2)$ :

(4) $\begin{equation*} (\hat{Y_1} - \hat{Y_2}) \pm 1.96 \times \sqrt{ \hat{SE}(Y_1)^2+ \hat{SE}(Y_2)^2}. \end{equation*}$

Now, let me describe the two approaches to determining statistical significance based on these intervals.

Two Ways to Determine Significance

The naïve method – the mistake I make all the time:

Examine whether the two confidence intervals (for $Y_1$ and $Y_2$ ) overlap.
Reject the null hypothesis if they do, and do not reject it otherwise.

The correct method:

Examine the confidence interval for the difference between the two quantities $(Y_1 - Y_2)$ .
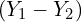Reject the null hypothesis if it does not contain 0, and do not reject it otherwise.

Digging a Bit Deeper

To understand why the naïve approach is wrong, let’s examine the length of these confidence intervals.

Under the naïve approach, the two confidence intervals overlap only if the following interval contains 0:

(5) $\begin{equation*} (\hat{Y_1} - \hat{Y_2}) \pm 1.96 \times (\hat{SE}(Y_1) + \hat{SE}(Y_2)). \end{equation*}$

This is the equation on which the decision under the naïve approach is based.

Let’s compare this expression with the confidence interval for the difference $(Y_1-Y_2)$ on which the decision under the correct approach is based.

Their ratio is equal to:

(6) $\begin{equation*} \frac{\hat{SE}(Y_1)+ \hat{SE}(Y_2)}{\sqrt{\hat{SE}(Y_1)^2 + \hat{SE}(Y_2)^2}}} \end{equation*}$

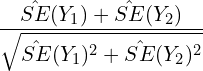
It is easy to see that this ratio is greater than one. In other words, the confidence interval in play under the naïve approach is wider than that under the correct approach.

Hence, when the two quantities are equal to each other (i.e., $H_0$ is true), the naïve method is more conservative (rejects less often; under rejects). When they are different ( $H_0$ is false), the naïve approach is less conservative (rejects too often; over rejects).

The discrepancy between the two methods will be largest when the ratio above is large. This happens when $\hat{SE}(Y_1)$ and $\hat{SE}(Y_2)$ are of equal value. The opposite is true as well – when one of $\hat{SE}(Y_1)$ and $\hat{SE}(Y_2)$ is much greater than the other, the ratio will roughly equal one, and hence the two methods will yield very similar results.

An Example

Schenker and Gentleman (2001) give a numerical example where $Y_1$ and $Y_2$ measure proportions. They set $\hat{Y}_1=.56$ , $\hat{Y}_2 = .44$ , $\hat{SE}(Y_1)=\hat{SE}(Y_2)=.0351$ .

In this case, the two confidence intervals for $Y_1$ and $Y_2$ are $[.49, .63]$ and $[.37, .51]$ , respectively. The two intervals overlap, so under the naïve approach, we conclude the two population proportions are not significantly different.

However, the confidence interval for the difference $(Y_1-Y_2)$ is $[.02, .22]$ . Clearly, it does contain 0, and thus, we cannot conclude statistical significance under the correct approach.

Bottom Line

Examining overlap in confidence intervals is an intuitive and natural way to judge statistical significance between two quantities.
While, in some cases, this naïve approach might give you the right answer, it is certainly not the correct way.
Instead, remember to analyze the confidence interval for the difference between the two quantities.

Where to Learn More

Check the paper by Schenker and Gentleman (2001) on which this post is based. The authors go deeper into this question with simulations and discussions on Type 1 errors and power.

References

Cole, S. R., & Blair, R. C. (1999). Overlapping confidence intervals. Journal of the American Academy of Dermatology, 41(6), 1051-1052.

Schenker, N., & Gentleman, J. F. (2001). On judging the significance of differences by examining the overlap between confidence intervals. The American Statistician, 55(3), 182-186.

yasenov.com