Background
Machine learning models are an indispensable part of data science. They are incredibly good at what they are designed for – making excellent predictions. They fall short in assessing the strength of the relationships they find. ML models make no reference to hypothesis testing, p-values, or anything else related to statistical significance. Why?
Several thorny challenges stand in the way. For starters, ML algorithms often scan the data multiple times to choose the best model (e.g., in selecting hyperparameters or choosing a few relevant variables). In the world of statistical inference, this is a bit like cheating since we have already selected the most strongly correlated variables.
Even if we can account for this (which we sometimes can), there is still the issue that ML models might make mistakes. For instance, regularization might force a model to exclude a variable that, in reality, belongs to the model with only a small coefficient. The t-stats and p-values of the remaining variables are potentially contaminated and unreliable. This might seem subtle, but overcoming it has proven challenging.
Researchers have made significant progress in assessing statistical significance in ML models in the past decade. This is exciting as it widens our understanding of how these so-very-commonly-used models work. We now have a wide variety of methods for hypothesis testing, and I will walk you through some of the most popular ones.
This field is often referred to as statistical inference after model selection. For simplicity, I will focus on linear models (and Lasso in particular), where we have the most exciting breakthroughs. Keep in mind that many methods generalize to other linear models – Ridge, Elastic net, SCAD, etc.
As a reminder, ![]() is the solution to:
is the solution to:
![]()
We are trying to predict a vector ![]() with a set of features
with a set of features ![]() with
with ![]() , and
, and ![]() is a tuning parameter. When needed, I will use
is a tuning parameter. When needed, I will use ![]() to index individual columns (variables) of
to index individual columns (variables) of ![]() .
.
Let’s get right into it.
Two Types of Models and Parameters
We first need to discuss an important subtlety. There are two distinct ways of thinking about performing hypothesis testing in ML models.
The traditional view is that we have a true linear model which includes all variables:
(1) ![]()
We are interested in testing whether ![]() – that is, inference on the full model. This is certainly an intuitive target. The interpretation is that this model encapsulates all relevant causal variables for
– that is, inference on the full model. This is certainly an intuitive target. The interpretation is that this model encapsulates all relevant causal variables for ![]() . Importantly, even if a given variable
. Importantly, even if a given variable ![]() is not selected, it still belongs to the model and has a meaningful interpretation.
is not selected, it still belongs to the model and has a meaningful interpretation.
There is an alternative way to think about the problem. Imagine we run a variable selection algorithm (e.g., lasso), which selects a subset ![]() of all available predictors (
of all available predictors (![]() ),
), ![]() leading to the alternative model:
leading to the alternative model:
(2) ![]()
Now we are interested in testing whether ![]() – that is, inference on the selected model. Unlike the scenario above, here
– that is, inference on the selected model. Unlike the scenario above, here ![]() is interpreted as the change in
is interpreted as the change in ![]() for a unit change in
for a unit change in ![]() when all other variables in
when all other variables in ![]() (as opposed to all of
(as opposed to all of ![]() ) are kept constant.
) are kept constant.
Which of the two targets is more intuitive?
Statisticians argue vehemently about this. Some claim that the full model interpretation is inherently problematic. It is too naïve and perhaps even arrogant to think that (i) mother nature can be explained by a linear equation, (ii) we can measure and include the full set of relevant predictors. On top of this, there are also technical issues with this interpretation beyond the scope of this post.
To overcome these challenges, relatively recently, statisticians developed the idea of inference on the selected model. This introduces major technical challenges, however.
Let us dive deeper and jump into the methods.
The Naïve Approach: What Not to Do
First things first – here is what we should not do.
- Run a Lasso regression.
- Run OLS regression on the subset of selected variables.
- Perform statistical inference with the estimated t-stats, confidence intervals, and p-values.
This is bad practice. Can you see why?
It is simply because we ignored the fact that we already peeked at the data when we ran the Lasso regression. Lasso already chose the variables that are strongly correlated with the outcome. Intuitively, we will need to inflate the p-values to account for the data exploration in the first step.
It turns out that, in general, both the finite- and large-sample distributions of these parameters are non-Gaussian and depend on unknown parameters in weird ways. Consequently, the calculated t-stats and p-values are all wrong, and there is little hope that anything simple can be done to save this approach. And no, the standard bootstrap cannot help us either.
But are there special cases when this approach might work? A recent paper titled “In Defense of the Indefensible: A Very Naïve Approach to High-Dimensional Inference” argues that under very strict assumptions on ![]() and
and ![]() , this method is actually kosher. The reason it works is that in the magical world of those assumptions, the set of variables that Lasso chooses is deterministic, and not random (hence circumventing the issue described above). The resulting estimator is unbiased and asymptotically normal – hence hypothesis testing is trivial.
, this method is actually kosher. The reason it works is that in the magical world of those assumptions, the set of variables that Lasso chooses is deterministic, and not random (hence circumventing the issue described above). The resulting estimator is unbiased and asymptotically normal – hence hypothesis testing is trivial.
Here is what we should do instead.
The Classical Approach: Inference on the Full Model
Roughly speaking, there are at least four ways we can go about doing hypothesis testing for ![]() in equation (1).
in equation (1).
Data Split
- Split our data into two equal parts.
- Run a Lasso regression on the first part.
- Run OLS on the second part with the selected variables from Step 2.
- Perform inference using the computed t-stats, p-values, and confidence intervals.
This is simple and intuitive. The problem is that in small samples, the p-values can be quite sensitive to how we split the data in the first step. This is clearly undesirable, as we will be getting different results every time we run this algorithm for no apparent reason.
Pros: Simple, intuitive, fast, and easy to explain to non-technical audiences.
Cons: Needs a lot of data and gives p-values only for selected variables.
Software package: We do not need any.
Multi Split
This is a modification of the Data Split approach designed to solve the sensitivity issue and increase power.
- Repeat
 times:
times:
- Reshuffle data.
- Run the Data Split method.
- Save the p-values.
- Aggregate the
 p-values into a single final one for each variable.
p-values into a single final one for each variable.
Instead of splitting the data into two parts only once, we can do it many times, and each time, we get a p-value for every variable. The aggregation goes a long way to solving the instability of the simple data split approach. There is a lot of clever mathematics behind it. For example, there is a complicated expression for aggregating the p-values rather than taking a simple average.
Pros: Simple, intuitive, sort of easy to explain to non-technical audiences.
Cons: Can be computationally expensive.
Software package: hdi
Bias Correction
This approach tackles the problem from a very different angle. The idea is to directly remove the bias from the naïve Lasso procedure without any subsampling or data splitting. Somewhat magically, the resulting estimator is unbiased and asymptotically normally distributed – statistical inference is then straightforward.
The are several versions of this idea, but the general form of these estimators is:
![]()
Where ![]() is the lasso estimator and
is the lasso estimator and ![]() are the residuals. The missing piece is the
are the residuals. The missing piece is the ![]() matrix; there are several ways to estimate it depending on the setting. In its simplest form, \hat{\Theta}is the inverse of the sample variance-covariance matrix. Other examples include the matrix, which minimizes an error term related to the bias as well as the variance of its Gaussian component.
matrix; there are several ways to estimate it depending on the setting. In its simplest form, \hat{\Theta}is the inverse of the sample variance-covariance matrix. Other examples include the matrix, which minimizes an error term related to the bias as well as the variance of its Gaussian component.
Similar bias-correction methods have been developed for Ridge regression as well.
Pros: Popular, simple, and sort of easy to explain to non-technical audiences.
Cons: N/A.
Software package: hdi
Bootstrap
As in many other complicated settings for statistical inference, the bootstrap can come to the rescue. Still, the plain vanilla bootstrap will not do. Instead, here is the general idea of the leading version of the bootstrap estimator for Lasso:
- Run a Lasso regression.
- Keep only
 ‘s larger than some magical threshold.
‘s larger than some magical threshold. - Compute the associated residuals and center them around 0.
- Repeat
 times:
times:
- draw random samples of these centered residuals,
- compute new responses
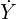 by adding them to the predictions
by adding them to the predictions  , and
, and - obtain
 coefficients from Lasso regressions on these new responses
coefficients from Lasso regressions on these new responses 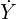 .
.
- Use the distribution of the obtained coefficients to conduct statistical inference.
This idea can be generalized to other settings and, for instance, be combined with the bias-corrected estimator.
Pros: N/A.
Cons: Challenging to explain to non-technical audiences.
Software package: N/A
This wraps up our discussion of methods for performing hypothesis testing on equation (1) (i.e., the full model). We now move on to a more challenging topic – inference on equation (2) (i.e., the selected model).
The Novel Approach: Inference on the Selected Model
PoSI (Post Selection Inference)
The goal of the PoSI method is to construct confidence intervals that are valid regardless of the variable selection method and the selected submodel. The benefit is that we would be reaching the correct conclusion even if we did not select the true model. This luxury comes at the expense of often being too conservative (i.e., confidence intervals are “too wide”). Let me explain how this is done.
To take a step back, most confidence intervals in statistics take the form:
![]()
Every data scientist has seen a similar formula before. The question is usually one about choosing the constant ![]() . When we work with two-sided hypotheses tests and large samples, we often use
. When we work with two-sided hypotheses tests and large samples, we often use ![]() because this is roughly the 97.5th percentile of the t-distribution with many degrees of freedom. This gives a 2.5% false positive error on both tails of the distribution (5% in total) and hence the associated 95% confidence intervals. The larger
because this is roughly the 97.5th percentile of the t-distribution with many degrees of freedom. This gives a 2.5% false positive error on both tails of the distribution (5% in total) and hence the associated 95% confidence intervals. The larger ![]() , the wider or more conservative the confidence interval.
, the wider or more conservative the confidence interval.
There are a few ways to choose the constant ![]() in the PoSI world. Vaguely speaking, PoSI says we should select this constant to equal the 97.5th percentile of a distribution related to the largest t-statistic among all possible models. This is usually approximated with Monte Carlo simulations. Interestingly, we do not need the response variable to approximate the value.
in the PoSI world. Vaguely speaking, PoSI says we should select this constant to equal the 97.5th percentile of a distribution related to the largest t-statistic among all possible models. This is usually approximated with Monte Carlo simulations. Interestingly, we do not need the response variable to approximate the value.
![]()
Another and even more conservative choice for ![]() is the Scheffe constant.
is the Scheffe constant.
![]()
where ![]() denotes the 95th percentile of the
denotes the 95th percentile of the ![]() distribution with the respective degrees of freedom.
distribution with the respective degrees of freedom.
Unfortunately, you guessed correctly that this method does not scale well. In some sense, it is a “brute force” method that scans through all possible model combinations and all variables within each model and picks the most conservative value. The authors recommend this procedure for datasets with roughly ![]() . This rules out many practical applications where machine learning is most useful.
. This rules out many practical applications where machine learning is most useful.
Pros: Valid regardless of whether or not we have selected the true model.
Cons: Does not work in high dimensions. Computationally very slow. Too conservative.
Software package: PoSI
EPoSI (Exact PoSI)
Ok, the name of this approach is not super original. The “E” here stands for “exact.” Unlike its cousin, this approach is valid only in the selected submodel. Because we cover fewer scenarios, the intervals will generally be narrower than the PoSI ones. EPoSI produces valid finite sample (as opposed to asymptotic) confidence intervals and p-values. Like all methods described here, the math behind this is extremely technical. So, I will give you only a high-level description of how this works.
The idea is first to get the conditional distribution of ![]() given the selected model. A bit magically, it turns out it is a truncated normal distribution. Really, who would have guessed this? Do you even remember truncated probability distributions (hint: they are just like regular PDFs but bounded from at least one side. This requires further scaling so that the density area sums to 1.)?
given the selected model. A bit magically, it turns out it is a truncated normal distribution. Really, who would have guessed this? Do you even remember truncated probability distributions (hint: they are just like regular PDFs but bounded from at least one side. This requires further scaling so that the density area sums to 1.)?
To dig one layer deeper, the authors show that the selection of Lasso predictors can be recast as a “polyhedral region” of the form:
![]()
In English, for fixed ![]() and
and ![]() , the set of alternative outcome values
, the set of alternative outcome values ![]() which yields the same set of selected predictors, can be expressed by the simple inequality above. In it,
which yields the same set of selected predictors, can be expressed by the simple inequality above. In it, ![]() and
and ![]() depend do not depend on
depend do not depend on ![]() . Under this new result, the distribution of
. Under this new result, the distribution of ![]() is now well-understood and tractable, thus enabling valid hypothesis testing.
is now well-understood and tractable, thus enabling valid hypothesis testing.
Then, we can use the conditional distribution function to construct a whimsical test statistic that is uniformly distributed on the [0,1] interval. And we can finally build confidence intervals based on that statistic.
Selective inference is currently among the hottest topic in all of statistics. There have been a myriad of extensions and improvements on the original paper. Still, this literature is painstakingly technical. What is the polyhedral selection property or a union of polytopes?
Pros: Theoretically rigorous. It’s a cool kids’ thing. Tons of theoretical work extends the idea to other settings.
Cons: Extremely technical.
Software package: selectiveInference
An Example
I used the popular Titanic dataset (n=889) to illustrate some of the methods I discussed above. Refer to the Kaggle website carefully for the descriptions of each variable. The outcome/response variable, survived, indicated whether the passenger survived the disaster (mean=0.382), while the predictors included demographic characteristics (e.g., age, gender) as well as some information about the travel ticket (e.g., cabin number, fare).
Unlike in Monte Carlo simulations, I do not know the ground truth here, so this exercise is not informative about which approaches work well and which do not. Rather, it just serves as an illustrative example.
You can find the code for this exercise here.
Here is a table displaying the number of statistically significant variables with ![]() -value < .05 for various inference methods.
-value < .05 for various inference methods.

As expected, the naive method results in the smallest p-values and hence the highest number of significant predictors – seven. Data Split knocks down two of those seven variables, resulting in five significant ones. The rest are more conservative, leaving only two or three features with ![]() < .05.
< .05.
Below is the table with p-values for all variables and each method.

Bottom Line
- Machine learning methods mine through datasets to find strong correlations between the response and the features. Quantifying this strength is an open and challenging problem.
- The naive approach to hypothesis testing is usually invalid.
- There are two main approaches that work – inference on the full model or on the selected model. The latter poses more technical challenges than the former.
- If we are interested in the full model, the Multi Split approach is general enough to cover a wide range of models and settings.
- If we believe you have to focus on the selected model, EPoSI is the state-of-the-art.
- Simulation exercises usually show no clear winner, as none of the methods consistently outperforms the rest.
Where to Learn More
Taylor and Tibshirani (2015) give a non-technical introduction to the problem space along with a description of the POSI method – a great read but focused on a single approach.
Other studies both provide a relatively accessible overview of the various methods for statistical inference on the full model.
For technical readers, Zhang et al. (2022) provide an excellent up-to-date review of the literature, which I used extensively.
References
Berk, R., Brown, L., Buja, A., Zhang, K., & Zhao, L. (2013). Valid post-selection inference. The Annals of Statistics, 802-837.
Bühlmann, P. (2013). Statistical significance in high-dimensional linear models. Bernoulli, 19(4), 1212-1242.
Dezeure, R., Bühlmann, P., Meier, L., & Meinshausen, N. (2015). High-dimensional inference: confidence intervals, p-values and R-software hdi. Statistical Science, 533-558.
Javanmard, A., & Montanari, A. (2014). Confidence intervals and hypothesis testing for high-dimensional regression. The Journal of Machine Learning Research, 15(1), 2869-2909.
Lee, J. D., Sun, D. L., Sun, Y., & Taylor, J. E. (2016). Exact post-selection inference, with application to the lasso. The Annals of Statistics, 44(3), 907-927.
Leeb, H., & Pötscher, B. M. (2005). Model selection and inference: Facts and fiction. Econometric Theory, 21(1), 21-59.
Leeb, H., Pötscher, B. M., & Ewald, K. (2015). On various confidence intervals post-model-selection. Statistical Science, 30(2), 216-227.
Meinshausen, N., Meier, L., & Bühlmann, P. (2009). P-values for high-dimensional regression. Journal of the American Statistical Association, 104(488), 1671-1681.
Taylor, J., & Tibshirani, R. J. (2015). Statistical learning and selective inference. Proceedings of the National Academy of Sciences, 112(25), 7629-7634.
Van de Geer, S., Bühlmann, P., Ritov, Y. A., & Dezeure, R. (2014). On asymptotically optimal confidence regions and tests for high-dimensional models. The Annals of Statistics, 42(3), 1166-1202.
Wasserman, L., & Roeder, K. (2009). High dimensional variable selection. Annals of Statistics, 37(5A), 2178.
Zhang, D., Khalili, A., & Asgharian, M. (2022). Post-model-selection inference in linear regression models: An integrated review. Statistics Surveys, 16, 86-136.
Zhang, C. H., & Zhang, S. S. (2014). Confidence intervals for low dimensional parameters in high dimensional linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 76(1), 217-242.
Zhao, S., Witten, D., & Shojaie, A. (2021). In defense of the indefensible: A very naive approach to high-dimensional inference. Statistical Science, 36(4), 562-577.
Leave a Reply