Background
Lasso is one of my favorite machine learning algorithms. It is so simple, elegant, and powerful. My feelings aside, Lasso indeed has a lot to offer. While, admittedly it is outperformed by more complex, black-box type of methods (e.g., boosting or neural networks), it has several advantages: interpretability, computational efficiency, and flexibility. Even when it comes to accuracy, theory tells us that under appropriate assumptions, Lasso can uncover the true submodel and we can even derive bounds on its prediction loss.
In this article I will briefly describe two ways researchers use Lasso to detect heterogeneous treatment effects. The underlying idea is to throw a bunch of covariates in the model and let the ![]() regularization do the difficult job of identifying which ones are important for treatment effect heterogeneity.
regularization do the difficult job of identifying which ones are important for treatment effect heterogeneity.
As always, let’s start with some notation. Let ![]() denote a binary treatment indicator,
denote a binary treatment indicator, ![]() be the potential outcomes under each treatment state (
be the potential outcomes under each treatment state (![]() is the observed one), and
is the observed one), and ![]() be a covariate vector. Lastly,
be a covariate vector. Lastly, ![]() is the share of units in the treatment group,
is the share of units in the treatment group, ![]() , where
, where ![]() is the sample size.
is the sample size.
The lasso coefficient vector is commonly expressed as the solution to the following problem:
(1) ![]()
where ![]() is the regularization parameter governing the variance-bias trade-off.
is the regularization parameter governing the variance-bias trade-off.
We are interested in the heterogeneous treatment effect given ![]() (
(![]() ):
):
(2) ![]()
That is, ![]() is the average treatment effect for units with covariate levels
is the average treatment effect for units with covariate levels ![]() .
.
More precisely, our goal is identifying which variables in ![]() divide the population of interest such that there are meaningful treatment effect differences in units across these groups. For instance, in the case of estimating the impact of school quality on test scores
divide the population of interest such that there are meaningful treatment effect differences in units across these groups. For instance, in the case of estimating the impact of school quality on test scores ![]() might be students’ gender (e.g., girls benefit more than boys), or in the context of online A/B testing
might be students’ gender (e.g., girls benefit more than boys), or in the context of online A/B testing ![]() might denote previous product engagement (e.g., tenured users benefit more from a new feature than inexperienced users).
might denote previous product engagement (e.g., tenured users benefit more from a new feature than inexperienced users).
Broadly speaking there are two main approaches of using Lasso to solve this problem – (i) a linear model with interactions between ![]() and
and ![]() , and (ii) directly regressing the imputed unit-level treatment effects on
, and (ii) directly regressing the imputed unit-level treatment effects on ![]() .
.
Let’s go over each one in detail.
Diving Deeper: Two Leading Methods
1. Lasso with Treatment Variable Interactions
In a low-dimensional world where regularization is not necessary and researchers are interested in ![]() s, they often use a linear model in which the treatment variable is interacted with the covariates. Statistically significant interaction coefficients identify the
s, they often use a linear model in which the treatment variable is interacted with the covariates. Statistically significant interaction coefficients identify the ![]() variables for which the treatment has differential impact.
variables for which the treatment has differential impact.
Mathematically, when all variables are properly interacted, this is analogous to splitting the sample into subgroups based on ![]() and running OLS on each group separately. This is feasible and convenient when
and running OLS on each group separately. This is feasible and convenient when ![]() is binary or categorical, but not when it is continuous. The advantage of this approach, however, is that the linear regression spits out
is binary or categorical, but not when it is continuous. The advantage of this approach, however, is that the linear regression spits out ![]() -values which can be (mis)used to determine statistical significance of these interaction variables.
-values which can be (mis)used to determine statistical significance of these interaction variables.
The OLS model is then:
(3) ![]()
where ![]() is the error term. The attention here falls on the coefficient vector
is the error term. The attention here falls on the coefficient vector ![]() which identifies whether the treatment has had a differential impact on units with a particular characteristic
which identifies whether the treatment has had a differential impact on units with a particular characteristic ![]() .
.
In high-dimensional settings when we have access to a wide vector ![]() , this is again not feasible. Instead, we might want to use an algorithm to pick out the variables in
, this is again not feasible. Instead, we might want to use an algorithm to pick out the variables in ![]() which are important for the treatment effect heterogeneity.
which are important for the treatment effect heterogeneity.
Imai and Ratkovic (2013) show us how to adapt the Lasso to this setting. It turns out you should not simply throw this model into the Lasso loss function. Can you guess why? Some variables might be predictive of the baseline outcome while others only of the treatment effect heterogeneity. The trick is to have two separate lasso constraints – ![]() and
and ![]() .
.
So, the loss function looks something like this:
(4) ![]()
A simplified version of the algorithm is as follows:
- Generate interaction variables,
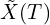 .
. - Run Lasso of
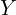 on
on 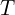 ,
,  and
and 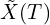 .
. - Identify statistically significant variables determining treatment effect heterogeneity.
A couple of notes. First, this requires some assurance that we are not overfitting, so that some form of sample splitting or cross validation is necessary. On top of this, Athey and Imbens (2017) suggest comparing these results with post-lasso OLS estimates to further guard against overfitting. Second, multiple testing is an issue as is the case with ML algorithms more generally. (You can check my earlier post on multiple hypothesis testing in linear machine learning models.) Options to take care of this include sample splitting and bootstrap, among others.
Software Package: FindIt.
2. Lasso with Knockoffs
An alternative approach directly regresses the unit-level treatment effects on ![]() . To get there, we first have to model the outcome function and impute the missing potential outcome for each unit. See my previous post on using Machine Learning tools for causal inference for more information on how we might do that.
. To get there, we first have to model the outcome function and impute the missing potential outcome for each unit. See my previous post on using Machine Learning tools for causal inference for more information on how we might do that.
This approach was developed by Xie et al. (2018). They recognized the multiple hypothesis issue and suggested using knockoffs to control the False Discovery Rate. This is still not completely kosher as it does not account for the fact that the outcome variable is estimated in an earlier step. Oh well. My guess and hope are that this is more of a theoretical concern, and empirically the inference we get is still “correct.”
Here is a simplified version of their algorithm:
- Transform the outcome variable
 .
. - Calculate unit-level treatment effects,
 .
. - Generate the difference
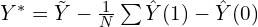 .
. - Run Lasso of
 on
on  and
and 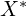 (the knockoff counterparts of
(the knockoff counterparts of  ).
). - Follow the knockoff method to obtain the set of significant variables.
Remember that ![]() has the special property that
has the special property that ![]() under the unconfoundedness assumption.
under the unconfoundedness assumption.
Interestingly, in the special case when ![]() the algebra reduces further which provides computation scaling advantages. Tian et al. (2014) showed this result first.
the algebra reduces further which provides computation scaling advantages. Tian et al. (2014) showed this result first.
An Example
I used the popular Titanic dataset (n=889) to illustrate the latter method. As such, it is a mere depiction of the approach, and its results should certainly not be taken seriously.
The outcome variable was survived, and the treatment variable was male. As is well known, women were much more likely to survive than men (74% vs 19% in this sample). So, I analyzed whether the gender difference in survival was impacted by other factors. I included the following covariates – pclass (ticket class), age, sibsp (number of siblings aboard), parch (number of parents aboard), fare, embarked (port of Embarkation), and cabin. Some of these were categorical in which case I converted them to a bunch of binary variables.
The knockoff filter identified a single variable as having a significant impact on the treatment effect – pclass. For the more affluent passengers (i.e., those in the higher ticket classes), this gender difference in survival was much smaller.
You can find the code in this GitHub repository.
Bottom Line
- The underlying idea behind using Lasso in
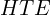 s estimation is to rely on
s estimation is to rely on  regularization to select which covariates are important for explaining differences in treatment responses. There are two main ways researchers use Lasso to estimate
regularization to select which covariates are important for explaining differences in treatment responses. There are two main ways researchers use Lasso to estimate 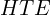 s.
s. - First, we can feed a linear model in which all covariates are interacted with the treatment indicator to the Lasso loss function with two separate regularization constraints.
- Second, we can directly regress the unit-level treatment effects on the covariates.
- I am not aware of any simulation studies comparing both approaches.
- While Lasso is among the simplest and most popular machine learning algorithms, there might be other, more suitable methods for estimating HTEs.
Where to Learn More
Hu (2022) is an excellent summary of the several ways researchers use Machine Learning to uncover heterogeneity in treatment effect estimation.
References
Barber, R. F., & Candès, E. J. (2015). Controlling the false discovery rate via knockoffs. The Annals of Statistics: 2055-2085.
Barber, R. F., & Candès, E. J. (2019). A knockoff filter for high-dimensional selective inference. The Annals of Statistics, 47(5), 2504-2537.
Chatterjee, A., & Lahiri, S. N. (2011). Bootstrapping lasso estimators. Journal of the American Statistical Association, 106(494), 608-625.
Hu, A. (2022). Heterogeneous treatment effects analysis for social scientists: A review. Social Science Research, 102810.
Imai, K., & Ratkovic, M. (2013). Estimating treatment effect heterogeneity in randomized program evaluation. The Annals of Applied Statistics (2013): 443-470.
Nie, X., & Wager, S. (2021). Quasi-oracle estimation of heterogeneous treatment effects. Biometrika, 108(2), 299-319.
Meinshausen, N., Meier, L., & Bühlmann, P. (2009). P-values for high-dimensional regression. Journal of the American Statistical Association, 104(488), 1671-1681.
Tian, L., Alizadeh, A. A., Gentles, A. J., & Tibshirani, R. (2014). A simple method for estimating interactions between a treatment and a large number of covariates. Journal of the American Statistical Association, 109(508), 1517-1532.
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288.
Wager, S., & Athey, S. (2018). Estimation and inference of heterogeneous treatment effects using random forests. Journal of the American Statistical Association, 113(523), 1228-1242.
Xie, Y., Chen, N., & Shi, X. (2018). False discovery rate controlled heterogeneous treatment effect detection for online controlled experiments. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (pp. 876-885).
Leave a Reply